

Home | Editorial | Astronomie | Aktuelles am Himmel | Sonstiges
Dieser Artikel beschreibt die optischen Grundlagen zu Teleskopen. Die überdurchschnittliche Länge des Artikels ist leider unvermeidlich, um die einzelnen Aspekte sinnvoll erklären zu können. Eine Aufteilung in mehrere Artikel wäre nicht sinnvoll gewesen, da sich sie einzelnen Unterthemen öfters aufeinander beziehen. Hier finden Sie den Artikel zu den mechanischen Grundlagen von Teleskopen.
Es gibt zwei Grundtypen von Spiegelteleskopen: Linsenteleskope (Refraktoren) und Spiegelteleskope (Reflektoren). Bei Refraktoren wird die lichtbrechende Eigenschaft von Linsen benutzt, um ein Bild im Brennpunkt zu erzeugen. Das ist das gleiche Prinzip, als wenn man mit einer Lupe ein Bild auf ein Blatt Papier projiziert. Spiegelteleskope nutzen Hohlspiegel (je nach Typ sphärische oder parabolische Spiegel) um das Licht im Brennpunkt zu bündeln. Ein Beispiel aus dem Alltag sind hier Vergrößerungsspiegel. Die verschieden einzelnen Teleskoptypen werden im Artikel "Teleskoptypen" detailliert beschrieben.
Das Hauptkriterium für das Leistungsvermögen eines Teleskops ist seine Öffnung. Sie entscheidet darüber, wieviel Licht das Teleskop sammelt. Je größer die Öffnung ist, umso schwächere Objekte können also grundsätzlich beobachtet werden. Mit der Öffnung steigt auch das Auflösungsvermögen des Teleskops, also seine Fähigkeit, eng benachbarte Details, zum Beispiel Doppelsterne oder Planetenstrukturen, als zwei Objekte darzustellen (siehe unten).
Die Lichtstärke wird vom Verhältnis Öffnung dividiert durch Brennweite ermittelt. Ist die Brennweite in Millimeter also z.B. sechsmal größer als die Öffnung in Millimeter, ist die Lichtstärke, auch Öffnungsverhältnis genannt, 1:6 bzw. f/6. Bei gegebener Öffnung nimmt die Lichtstärke mit zunehmender Brennweite also ab. Die Brennweite ist die Strecke zwischen lichtsammelnder Fläche (Linsenmittelpunkt oder Spiegelfläche) und dem Brennpunkt. Die folgende Grafik veranschaulicht diese beiden Grundgrößen von Teleskopen am Beispiel eines Refraktors:
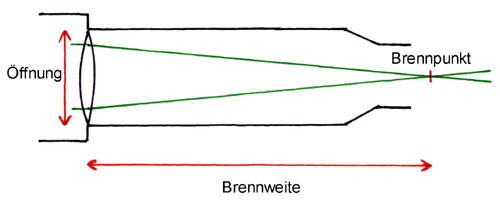
Lichtschwache Objekte und solche mit geringer Flächenhelligkeit sind mit lichtstarken Teleskopen einfacher zu beobachten. Das liegt daran, dass sie mit größerer Austrittspupille (berechnet aus Durchmesser der Optik in Millimeter dividiert durch die Vergrößerung) mit größerer Helligkeit erscheinen. Mit abnehmender Lichtstärke, also zunehmender Brennweite werden immer langbrennweitigere Okulare benötigt, um die erforderlichen großen Austrittspupillen zu erreichen. Bei zu geringen Lichtstärken sind maximale Austrittspupillen oft gar nicht möglich. Die steigende Lichtstärke bringt allerdings auch den Nachteil mit sich, dass physikalisch bedingte Abbildungsfehler wie Farbfehler beim Refraktor oder die Koma beim Reflektor deutlicher erkennbar oder bei hohen Lichtstärken sogar extrem störend werden.
Das Lichtsammelvermögen sagt lediglich aus, wieviel Licht eine gegebene Optik sammelt. Es hängt ausschließlich von der lichtsammelnden Fläche und nicht von der Lichtstärke der Optik ab. Bei obstruierten Systemen muss man zur Berechnung der lichtsammelnden Fläche die Obstruktionsfläche von der Fläche der Primäroptik abziehen. Um ihr Lichtsammelvermögen zu verdoppeln, muss man den Durchmesser der Fläche um den Faktor 1,4 erhöhen. Eine Verdoppelung des Durchmessers bewirkt ein vierfaches Lichtsammelvbermögen.
Das Lichtsammelvermögen wird stets sinnvollerweise im Verhältnis zu einer Bezugsgröße, in der Regel die maximale Pupillenöffnung des menschlichen Auges, angegeben, um aussagekräftige Werte zu erhalten. Das sind etwa sieben Millimeter. Die lichtsammelnde Fläche beträgt hier also 38,47 Quadratmillimeter. Ein Teleskop mit 20 Zentimeter freier Öffnung hat eine Lichtsammelfläche von 32.349 Quadratmillimeter, also ein 841-faches Lichtsammelvermögen gegenüber dem bloßen Auge. Solche Angaben sind letztendlich Richtwerte, da die exakte maximale Pupillenöffnung von Mensch zu Mensch verschieden ist.
Die Grenzgröße gibt an, wie hell die schwächsten Sterne sind, die mit einem gegebenen Teleskop noch erkannt werden können. Sie hängt direkt mit dem Lichtsammelvermögen zusammen: Je größer es ist, umso schwächere Sterne sind sichtbar. Man unterscheidet die visuelle von der fotografischen Grenzgröße: Die visuelle gibt an, welche Sternhelligkeiten in mag bei der visuellen Beobachtung unter Verwendung der förderlichen Vergrößerung noch beobachtbar sind. Die fotografische Grenzgröße macht die gleiche Angabe für ausbelichtete Astrofotos, also die schwächsten Sterne, die eben noch auf Fotos mit dem betreffenden Teleskop sichtbar sind. Die fotografische Grenzgröße ist erfahrungsgemäß ca. 2,5 mag schwächer als die visuelle, da der Bildsensor Licht sammelt.
Die Angaben der Grenzgröße gelten nur für Sterne, da nur bei ihnen das Licht auf eine Punktquelle konzentriert ist. Für flächige Objekte, also Nebel, Galaxien und Kometen, gilt sie nicht (deshalb wird manchmal auch von "stellarer Grenzgröße" gesprochen). Hat ein Nebel eine bestimmte Helligkeit, beispielsweise 6,0 mag, bedeutet dies, dass seine Helligkeit der eines 6,0 mag-Sterns entspricht, dessen Licht auf die Fläche des Nebels verteilt ist. Umgekehrt ausgedrückt hätte ein Stern, der resultieren würde, wenn man das Licht des Nebels auf einen Punkt konzentrieren könnte, eine Helligkeit von 6,0 mag. Die folgende Tabelle gibt die visuelle und fotografische Grenzgröße für einige gängige Teleskopöffnungen an.
| Öffnung in mm | Visuelle Grenzgrösse | Fotografische Grenzgrösse |
| 70 | 11,0 mag | 13,5 mag |
| 90 | 11,5 mag | 14,0 mag |
| 102 | 12,1 mag | 14,6 mag |
| 114 | 12,7 mag | 15,2 mag |
| 127 | 13,2 mag | 15,7 mag |
| 152 | 13,6 mag | 16,1 mag |
| 203 | 14,0 mag | 16,5 mag |
| 254 | 14,5 mag | 17,0 mag |
| 305 | 15,0 mag | 17,5 mag |
| 406 | 15,6 mag | 18,1 mag |
Die Werte sind jedoch keine absoluten Zahlen, sondern theoretischer Natur: Die tatsächliche Grenzgröße eines Teleskops hängt von weiteren Faktoren ab. Zunächst sei hier die bereits erwähnte Obstruktion erwähnt. Beispielsweise hat ein Maksutov-Spiegelteleskop mit 90 Millimeter Öffnung eine etwas geringere Grenzgröße als ein Refraktor mit der gleichen Öffnung. Weitere Faktoren, die die Grenzgröße herabsetzen können sind der Reflexionsgrad der verwendeten Spiegel und die Transmission von Teleskop- und sogar der Okularlinsen. Vergleichstests belegen immer wieder, dass Okulare je nach verwendeter Glassorten die Grenzgröße merklich beeinträchtigen.
Die Auflösung, auch Trennschärfe genannt, ist die Fähigkeit eines Teleskops, eng benachbarte Details, zum Beispiel Doppelsterne oder Planetenstrukturen, als zwei Objekte darzustellen. Sie steigt mit der Öffnung des Teleskops und hängt ausschließlich von dieser ab. Eine evtl. vorhandene Obstruktion hat im Gegensatz zur Grenzgröße keinen Einfluss auf die Auflösung. Physikalisch bedingte Abbildungsfehler wie die Koma oder Bildfeldwölbung können die Auflösung abseits der optischen Achse, also der Bildmitte, deutlich herab setzen. Letztendlich hängt die maximale Trennschärfe auch vom Justagezustand und der Optikqualität ab.
Zum Verständnis der nachfolgenden Erklärungen sei erläutert, wie sich die Beugung des Lichts an Hindernissen wie Spiegel- und Linsenfassungen und an der Fangspiegelaufhängung optisch auswirkt. Es entsteht ein zentrales Beugungsscheibchen, das den Stern repräsentiert. Gebeugtes Licht wandert in die sog. Beugungsringe. Dies sind die bei hohen Vergrößerungen sichtbaren konzentrischen Ringe um das Beugungsscheibchen. Ihr Abstand untereinander und vom äüßeren Rand des Beugungsscheibchens entspricht der Auflösung des Teleskops in Bogensekunden. Das Beugungsscheibchen hat den gleichen Durchmesser wie das Auflösungsvermögen des Teleskops. Mit zunehmender Öffnung und Auflösung wird das Beugungsscheibchen entsprechend kleiner (mehr Öffnung = höhere Auflösung), und folglich können enger beieinander stehende Details aufgelöst werden.
Mit zunehmender Obstruktion wächst der Anteil des Lichts, das in die Beugungsringe geht, dem Stern geht also Licht verloren. Aus diesem Grund haben obstruierte Systeme einen etwas geringeren Kontrast als nicht obstruierte Teleskope. Bei Obstruktionen unter etwa 30 Prozent ist dieser Kontrastverlust jedoch marginal. Das Beugungsscheibchen selbst nimmt jedoch mit zunehmender Obstruktion im Durchmesser ab.
Es gibt zwei Definitionen der Auflösung, die auf verschiedenen Vorstellungen bzw. Auslegungen basieren: Das Rayleigh- und das Dawes-Kriterium.
Nach Dawes sind zwei Sterne aufgelöst, wenn der Mittelpunkt des einen Beugungsscheibchens exakt auf dem Rand des benachbarten zu liegen kommt. Die Folge ist eine sehr schwache Einbuchtung zwischen den Beugungsscheibchen, die nur bei exzellenten Bedingungen erfasst werden kann. Die Faustformel für den Abstand zweier Sterne in Bogensekunden, die nach Dawes bei gegebener Öffnung eben noch getrennt werden können, lautet:
a (alpha) = 11,3 / D (a = Auflösung in Bogensekunden; D = Öffnung in Zentimeter)
Dieses Kriterium wird in der Regel in Produktbeschreibungen verwendet, da es höhere Auflösungen ergibt als nach dem Rayleigh-Kriterium. Beim strengeren Rayleigh-Kriterium sind zwei Sterne getrennt, wenn die Mitte des Beugungsscheibchens des einen Sterns genau zwischen dem zweiten und seinem innersten Beugungsring zu liegen kommt. Die Einbuchtung zwischen den beiden Beugungsscheibchen ist hier deutlicher zu erkennen. Die Faustformel für den Abstand zweier Sterne, die nach Rayleigh bei gegebener Öffnung eben noch getrennt werden können, lautet:
a (alpha) = 13,8 / D (a = Auflösung in Bogensekunden; D = Öffnung in Zentimeter)
Es bleibt also eine Frage der Interpretation, ab wann ein Doppelstern aufgelöst ist. Die physikalischen Hintergründe lassen sich auf der folgenden Seite nachlesen: www.greier-greiner.at/hc/aufloesung.htm
Das folgende Diagramm zeigt die Auflösung als Funktion der Öffnung in Millimeter. Es wurde hier das Dawes-Kriterium als Grundlage gewählt, da es in Produktbeschreibungen öfters verwendet wird. Ein Klick auf die Grafik öffnet die große Version.
Eine Vergütung hat drei Aufgaben: Sie soll störende Reflexe reduzieren, die Transmission (Lichtdurchlässigkeit) erhöhen, indem die Rückstreuung von einfallendem Licht unterdrückt wird und die Anfälligkeit für Kratzer reduzieren. Aus letzterem Grund werden einige moderne und teure Vergütungen öfters als "Hartvergütung" bezeichnet, da sie härter sind als das Objektivglas. Die Vergütung einer Brille wird als "Entspiegelung" bezeichnet. Eine Vergütung, die sich aus mehreren übereinander liegenden Schichten zusammen setzt, wird Multivergütung genannt. Es gibt bei Teleskopen drei Grundtypen von Vergütungen, die sich durch ihre Farbe unterscheiden:
Blaue Vergütungen sind die einfachsten, preiswertesten aber auch anfälligsten. Sie findet sich heutzutage auf praktisch jedem noch so preiswerten optischen Erzeugnis. Sie ist offenbar anfällig für unsachgemäße Reinigungen. Einigen Erfahrungsberichten zufolge wurde sie schon bei der Reinigung mit speziellen Reinigungsmitteln entfernt. Grüne Vergütungen haben bereits eine bessere Qualität und Haltbarkeit. Sie finden sich auf optischen Geräten der mittleren Preisklasse. Violette Vergütungen sind die qualitativ hochwertigsten. Sie finden sich auf hochwertigen Ferngläsern und Teleskopen. Häufig werden sie als Multivergütung ausgeführt. Das Foto zeigt eine Vergütung am Beispiel einer grünen Vergütung eines Fernglasobjektivs:
Die für astronomische Beobachtungen benötigten Vergrößerungen werden von Anfängern oft falsch eingeschätzt. Hohe Vergrößerungen werden nur selten bzw. bei bestimmten Objekten, wie zum Beispiel Mond und Planeten benötigt. Weitaus häufiger werden Vergrößerungen gebraucht, die im mittleren Bereich bis zur minimal sinnvollen Vergrößerung eines Geräts anzusiedeln sind.
Die Vergrößerung eines Teleskops oder Fernglases errechnet sich aus der Objektiv- bzw. Spiegelbrennweite dividiert durch die Okularbrennweite:
V = F(Objektiv) / f(Okular)
Bei einem Teleskop kann man die Vergrößerung also nur durch den Wechsel der Okularbrennweite und ggf. der Vorschaltung von Barlow-Linsen oder Focal-Reducern verändern. Das Okular ist nichts anderes als eine stark vergrößernde Lupe, mit der das vom Objektiv bzw. Spiegel im Fokus erzeugte reelle Bild betrachtet wird.
Aus obiger Formel ergibt sich, dass man rein rechnerisch mit entsprechend langen oder kurzen Okularbrennweiten jede beliebige Vergrößerung erzeugen kann. Bei der Anwendung extremer Vergrößerungen gibt es jedoch physikalische Grenzen zu beachten. Hier werden drei besondere Vergrößerungen unterschieden:
Die maximal sinnvolle Vergrößerung ist die Vergrößerung, ab der das Bild dunkel und kontrastarm wird und an Schärfe verliert. Sie hängt letztendlich von der Fertigungsqualität der Optik ab. Bei hochwertigen Teleskopen beträgt sie etwa das Doppelte des Objektiv- bzw. Spiegeldurchmessers in Millimetern.
Die ab dieser Vergrößerung auftretenden Schärfeverluste sind neben der Fertigungsqualität in erster Linie auf Beugungsunschärfen zurück zu führen, die durch die Linsenfassung, Spiegelränder und Fangspiegelaufhängung entstehen und daher unvermeidlich sind.
Diese maximal sinnvolle Vergrößerung wird in den allermeisten Fällen aufgrund atmosphärischer Störungen, insbesondere des Seeings, nicht nutzbar sein. Unabhängig von obiger Definition wird die maximal sinnvolle Vergrößerung also meist durch die Luftruhe und Qualität der atmosphärischen Bedingungen bestimmt.
Sie ist nicht mit der förderlichen Vergrößerung (siehe unten) zu verwechseln.
Die förderliche Vergrößerung ist die Vergrößerung, ab der das theoretische Auflösungsvermögen eines Teleskops ausgeschöpft wird. Sie entspricht etwa dem Objektiv- bzw. Spiegeldurchmesser in Millimetern. Eine weitere Vergrößerung zeigt keine weiteren Details. Die vorhandenen Strukturen erscheinen dann jedoch größer und treten deutlicher hervor.
Die folgende Grafik demonstriert schematisch den Unterschied zwischen förderlicher Vergrößerung und einer höheren Vergrößerung im Bereich der maximal sinnvollen Vergrößerung an einem fiktiven Doppelstern. Zu Gunsten einer besseren Übersicht wurde auf die Darstellung der Beugungsringe verzichtet.
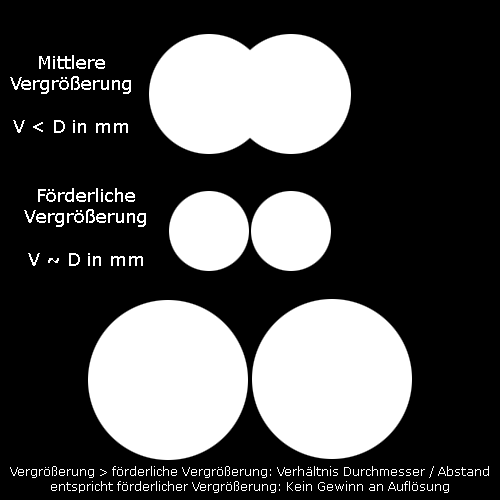
Die obige Abbildung zeigt den Doppelstern bei schwacher bis mittlerer Vergrößerung (V kleiner als der Objektivdurchmesser in Millimetern). Er ist zwar schon als solcher zu erkennen, jedoch noch nicht vollständig getrennt.
Die mittlere Abbildung sei bei der förderlichen Vergrößerung entstanden. Der Doppelstern ist vollständig mit einem schmalen Zwischenraum zwischen den beiden Komponenten getrennt. Die der Anschaulichkeit halber extrem vergrößerten Beugungsscheibchen der Sterne haben in der Grafik 80 Pixel und der Zwischenraum zwei Pixel Ausdehnung.
Die untere Abbildung zeigt den Doppelstern bei sehr starker Übervergrößerung gegenüber der förderlichen Vergrößerung. Die Sterne haben jetzt 160 Pixel und der Zwischenraum vier Pixel Ausdehnung. Das Bild wurde also als Ganzes vergrößert, und der Zwischenraum ist deutlicher und angenehmer zu erkennen. Ein Auflösungsgewinn wurde nicht erzielt. Bei besserer Auflösung wären in der dritten Abbildung die Sternscheibchen kleiner und der Zwischenraum größer als in der mittleren Abbildung.
Bei der Beobachtung von Mond, Planeten und Doppelsternen kann es also je nach Seeing durchaus sinnvoll sein, über die förderliche Vergrößerung hinaus zu vergrößern. Details an der Grenze der Auflösung sind dann angenehmer und leichter zu erkennen. Teleskopbeobachter, die aufgrund von Astigmatismus (Hornhautverkrümmung) eine Brille tragen, müssen erfahrungsgemäß stärker vergrößern, um die gleichen Details zu erkennen, die ein astigmatismus-freies Auge bei schwächerer Vergrößerung erkennt.
Die minimal sinnvolle Vergrößerung ist die Vergrößerung, bei der die Austrittspupille (siehe unten), sieben Millimeter Durchmesser hat. Das entspricht etwa der Pupillenöffnung des menschlichen Auges bei maximaler Dunkeladaption.
Eine Faustformel für die minimal sinnvolle Vergrößerung ist der Durchmesser des Objektiv bzw. Sipegels in Millimeter dividiert durch sieben, also
V = D / 7.
Die minimal sinnvolle Vergrößerung bewirkt auch gleichzeitzig die maximal mögliche Bildhelligkeit des verwendeten Geräts: Bei größerer Austrittspupille kann das Licht vom Rand selbiger nicht mehr ins Auge gelangen, da die Pupille des Auges maximal sieben Millimeter geöffnet ist. Es wird also Licht verschenkt und das Lichtbündel durch die Pupille "abgeblendet".
Auch hier gibt es eine Einschränkung, und die wird durch die (künstliche) Himmelsaufhellung gesetzt. Ein Erfahrungswert besagt, dass die Austrittspupille in Millimeter nicht größer sein sollte als die Helligkeit der schwächsten Sterne, die mit dem bloßen Auge sichtbar sind. Bei einer visuellen Grenzgröße von 5 mag sollte die Austrittspupille also nicht größer als fünf Millimeter sein. Bei größeren Austrittspupillen wird der Himmelshintergrund im Okular aufgehellt, und schwächere Objekte sind dann nicht mehr erkennbar.
In solch einem Fall lautet die Formel für die minimal sinnvolle Vergrößerung
V = D / AP
(AP = Austrittspupille, entspricht der visuellen Grenzgröße; D = Durchmesser der Optik in Millimeter).
Aus der Formel für die Austrittspupille (siehe unten) geht hervor, dass die minimal sinnvolle Vergrößerung mit der Öffnung zunimmt.
Die Austrittspupille (AP) ist im Zusammenhang mit Fernglas- und Teleskopbeobachtungen der Durchmesser des Lichtbündels, das das Okular verlässt. Man erkennt sie am besten als einen hellen Kreis, wenn man die Optik gegen eine helle Fläche, zum Beispiel den Taghimmel, hält. Die Austrittspupille berechnet sich aus folgenden Formeln:
AP = D / V;
D = Durchmesser von Linse bzw. Spiegel im Millimeter; V = Vergrößerung, oder
AP = Okularbrennweite / Nenner des Öffnungsverhältnisses (z.B. 6 bei f/6)
Aus der Tatsache, dass die AP ein Maß für die das Auge erreichende Lichtmenge ist, geht unmittelbar hervor, dass das Bild mit kleiner werdender AP und damit mit steigender Vergrößerung bei gegebener Öffnung dunkler wird.
Letzendlich bestimmt nur die Austrittspupille, wie hell das Bild eines bestimmten Objekts, zum Beispiel des Mondes, im Okular erscheint. Bei gleicher AP erscheint er stets gleich hell, unabhängig von Telesklop, Öffnung und Vergrößerung.
Das Foto zeigt die Austrittspupille am Beispiel eines 12*60-Feldstechers. Für die Aufnahme wurde das Fernglas auf einen leicht bedeckten Taghimmel gerichtet, um die Austrittspupille deutlich sichtbar zu machen. Bei astronomischen Beobachtungen findet sich an der Stelle des hellen Kreises ein Abbild des vom Beobachtungsgerät erfassten Sternenhimmels, das aufgrund seiner Helligkeit natürlich so nicht direkt sichtbar ist.
Jedes astronomische Beobachtungsgebiet hat bestimmte Austrittspupillen, bei denen eine optimale Abbildung erzeugt wird. In diesem Punkt sind Austrittspupillen zur Frage nach der besten Abbildung besser geeignet als Vergrößerungen, da sich mit ihnen die Abbildungen verschiedener Teleskope direkt vergleichen lassen: Gleiche Austrittspupillen bedeuten wie bereits gesagt unabhängig von der Öffnung die gleiche Bildhelligkeit, und die Austrittspupille ist bei verschiedenen Teleskopen nicht an eine bestimmte Vergrößerung gekoppelt.
Die für die jeweilige Anwendung optimale Vergrößerung V lässt sich für die verwendete Teleskopöffnung D (in Millimeter) direkt aus der Formel
V = D / AP
errechnen.
Für Deep Sky-Beobachtungen eignen sich große bis mittlere AP's. Prinzipiell sollte hier eine möglichst große AP gewählt werden, um eine möglichst große Bildhelligkeit zu ermöglichen. Das gilt insbesondere für ausgedehnte Objekte mit geringer Flächenhelligkeit, zum Beispiel ausgedehnte Gasnebel. Bei detailreichen Objekten, zum Beispiel Kugelsternhaufen, Galaxien oder Planetarische Nebel, kann man auch bei mittlerer AP etwas höher vergrößern. Für Galaxien hat sich eine AP von ca. zwei Millimeter bewährt.
Mond, Planeten und Doppelsterne sind detailreiche Objekte, bei denen man stark vergrößern kann. Planeten sind zudem kontrastarme Objekte. Hier hat sich eine AP von 0,8 bis 0,7 Millimeter bewährt. Diese Vergrößerung gewährt einen guten Kontrast, und der Planet erscheint zumindest bei mittleren Teleskopöffnungen bereits angenehm groß. Solch kleine AP's lassen sich natürlich nur bei gutem Seeing anwenden. Bei großen Austrittspupillen erscheinen Mond und Planeten oft blendend hell, so dass kontrastarme und/oder feine Details oft überstrahlt und damit unbeobachtbar werden. Es wird somit eine geringere Auflösung des Teleskops vorgegaukelt. Erlaubt das Seeing keine kleineren AP's und damit hohe Vergrößerungen, lässt sich die Erkennbarkeit von Details durch die Anwendung von Neutralgrau- oder Farbfiltern erheblich steigern.
Ergänzend sei gesagt, dass bei guten Augen ab einer Austrittspupille kleiner als ein Millimeter die physikalisch bedingten Beugungsunschärfen bemerkbar werden. Die besagten Austrittspupillen befinden sich also im Grenzbereich zur Beugungsunschärfe. Sie nutzen die Vergrößerungsfähigkeit einer qualitativ hochwertigen Optik also optimal aus.
Das Gesichtsfeld ist die Fläche des Himmels, die man beim Blick durch ein Fernrohr oder Fernglas beobachten kann. Die Bedeutung eines großen Gesichtsfeldes wird von Anfängern oft unterschätzt. Mit einem großen Gesichtsfeld lassen sich Himmerlsobjekte, nachdem sie im Sucher angepeilt wurden, wesentlich einfacher auffinden und zentrieren als mit kleinen Gesichtsfeldern. Viele Objekte im Deep Sky-Bereich sind so großflächig, dass sie sich mit mittleren und großen Teleskopen wenn überhaupt nur mit dem größtmöglichen Gesichtsfeld vollständig überblicken lassen. Nichts zuletzt steigt die Bildhelligkeit bei einer gegebenen Optik mit der Größe des Gesichtsfeldes.
Ein großes Gesichtsfeld hat aber auch Nachteile:
Am Gesichtsfeldrand zeigen sich Randunschärfen und physikalisch bedingte Abbildungsfehler, zum Beispiel Koma bei Newton-Teleskopen, viel Stärker als zur Mitte des Bildes hin. Ein großes Gesichtsfeld ist also am Rand fehleranfälliger als ein kleines. Gute Okulare, die ein sehr großes Gesichtsfeld bei gleichzeitig guter bis sehr guter Randabbildung ermöglichen, sind sehr teuer. Am Gesichtsfeldrand zeigt sich auch oft eine Randabdunkelung des Bildes, die sog. Vignettierung.
Die Größe des Gesichtsfeldes hängt von folgenden Faktoren ab: Brennweite, Vergrößerung (Okularbrennweite), Eigengesichtsfeld des Okulars, Steckdurchmesser des Okularauszugs und das optische Design. Um große Gesichtsfelder zu erzielen, benötigt man eine nicht zu lange Brennweite, eine lange Okularbrennweite sowie ein Okular mit großem Eigengesichtsfeld (sog. Weitwinkelokulare) mit 2'' Steckhülse (bei guter Qualität sehr teuer) und einen entsprechenden Okularauszug.
Bei Vergrößerungen gilt die Grundregel: Weniger ist mehr. Es macht keinen Sinn, stets um jeden Preis die größtmögliche Vergrößerung zu wählen, die die Ausrüstung hergibt. Auch bei Mond und Planeten ist selbst die förderliche Vergrößerung aufgrund des Seeings gerade bei großen Teleskopöffnungen oft nicht mehr sinnvoll. In diesem Fall ist mitunter ein Neutralgraufilter erforderlich, da feine Details sonst überstrahlt werden.
Eine Beobachtung wird stets mit der schwächsten Vergrößerung begonnen. Mit dieser wird das Objekt aufgesucht und zentriert.
Für lichtschwache oder ausgedehnte Objekte wäre eine wesentlich stärkere Vergrößerung wenig sinnvoll, da die Bildhelligkeit mit der Vergrößerung abnimmt und das Objekt mitunter nicht mehr komplett ins Gesichtsfeld passt. Nachdem das Objekt bei schwächster Vergrößerung eingestellt und zentriert wurde, kann man sich mit stärkeren Vergrößerungen dem Objekt nähern, bis man die optimale Vergrößerung gefunden hat, die ein bestmöglichstes und angenehmstes Bild liefert. Diese optimale Vergrößerung hängt natürlich auch von den jeweiligen atmosphärischen Bedingungen (Seeing und Dunst) ab.